Föreläsning i flervariabelanalys
Föreläsning om Lagranges Multiplikatormetod
Lagrange multiplikatormetod hjälper oss att lösa maximi/minimiproblem när vi är max/min punkterna är tvingade att uppfylla ett extra bivillkor.
Till föreläsningenFöreläsningens innehåll
I denna föreläsning går vi igenom Lagranges multiplikatormetod. Denna metod är användbar när den funktion som sak maximeras/minimeras
givet ett extra villkor. Ett exempel kan vara att vi söker minsta avstånd till origo från en viss nivåyta till en viss funktion.
Dessa problem kan ofta vara svåra att lösa med mera direkta metoder och då erbjuder Lagrangemetod ett alternativ.
Föreläsningen motiverar metoden utifrån ett exempel. Formulerar sedan metoden och löser sedan exemplet med metoden.
Sist ges ett ytterligare exempel (som är en tolkning av Adams uppgift 13.3.18)
Avsnitt i Adams att arbeta med
Detta material svarar mot kapitel 13.3 i Adams.
Uppgifter från Adams att räkna
13.3 :: 1, 3, 5, 5, 7, 9, 11, 13
Räkneövningar kopplade till denna föreläsning
Miniföreläsningar kopplade till denna föreläsning
- Lagrange exempel Adams 13.3.4::
Till miniföreläsningen
sammanfattning:
Lösning till Adams uppgift 13.3.4. Ett exempel på Lagranges multiplikatormetod.
Lösta problem knutna till denna föreläsning
- Uppgift om Lagrange multiplikator-metod.::
Svar/lösning
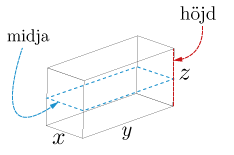
Ett postföretag levererar bara paket i form av rektangulära lådor med midja och höjd uppfyller vissa villkor. Midjan är omkretsen av ett horisontellt tvärsnitt. (Se figur nedan) Vilkoret som paketet måste uppfylla är att summan av midjan och paketets höjd får vara högst 120 cm. Beräkna den största volym som en sådan låda kan ha.
Mathematica dokument för denna föreläsning ::
För närvarande finns inga mathematicadokument producerade för denna föreläsning.
Veckoplaneringar :
Terminologi:: En vekka är för en kvartsfartskurs
två vanliga veckor.