Flervariabelanalys
övningsexempel
Lösta Problem
Lösta problem är en samling exempel med svar och lösningar som kompletterar kursbokens uppgifter. Många av uppgifterna har förekommit på gamla tentamina vilket innebär att denna problemsamling i någon mån definierar kursens nivå.
P
Min max uppgift
Detta problem hör ihop med föreläsning 6 :: Andraderivatatestet för klassificering av kritiska punkter
Uppgift ::
Svar ::
Lösning ::
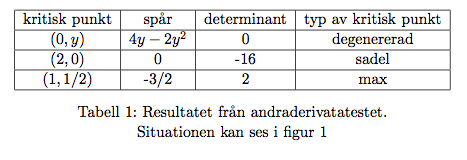
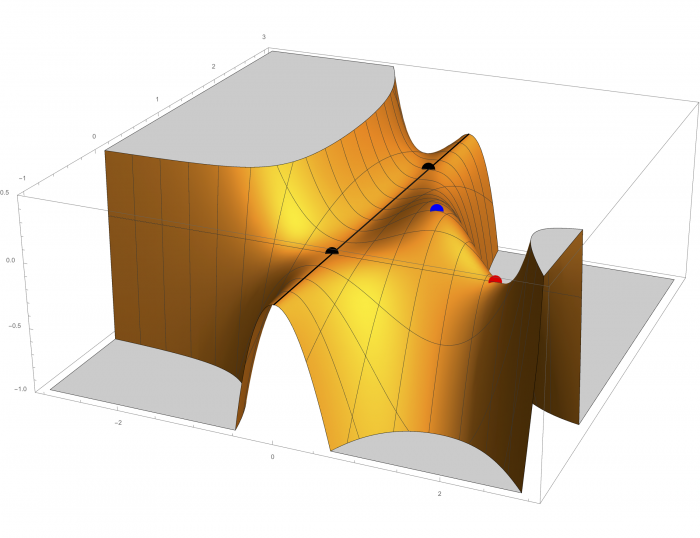 Kritiska punkterna \((0,y)\) ligger på den svarta linjen och vi har att funktionen är konstant på denna linje.
Detta gör att vi på den svarta linjen inte har strikta max, min eller sadelpunkter.
Tittar man noggrant så ser vi att för varje fixt \(y\) så är andra derivatan map \(x\) lika med \(2y(2-y)\) och denna
derivata är positiv om \(0
Kritiska punkterna \((0,y)\) ligger på den svarta linjen och vi har att funktionen är konstant på denna linje.
Detta gör att vi på den svarta linjen inte har strikta max, min eller sadelpunkter.
Tittar man noggrant så ser vi att för varje fixt \(y\) så är andra derivatan map \(x\) lika med \(2y(2-y)\) och denna
derivata är positiv om \(0Uppgift om Lagrange multiplikator-metod.
Detta problem hör ihop med föreläsning 7 :: Föreläsning om Lagranges Multiplikatormetod
Uppgift ::
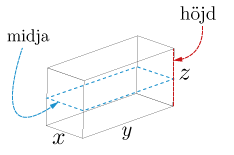
Svar ::
Lösning ::
Tangentplan för en funktionsgraf
Detta problem hör ihop med föreläsning 3 :: Derivatamatriser och kedjeregler
Uppgift ::
Svar ::
Lösning ::
Om vi vill skriva tangentplanet på parameterform så kan vi enligt räkneövning 4 använda partialderivatorna till funktionsgrafens parametrisering men innan vi kan göra det så behöver vi beräkna en sådan parametrisering av funktionsgrafen. Detta är ganska enkelt i vårt fall: sätt \(x=u\) och \(y=v\) och \(z=f(x,y)=f(u,v)=u^2-v^2\): \[ S(u,v)=(u,v,f(u,v))=(u,v,u^2-v^2) \] Partialderivatorna blir därför \[ \begin{split} \frac{\partial S}{\partial u}\Bigg|_{(1,2)}&=\left[\begin{array}{c}1 \\0 \\2u\end{array}\right]_{(1,2)}=\left[\begin{array}{c}1 \\0 \\2\end{array}\right] \\ \frac{\partial S}{\partial v}\Bigg|_{(1,2)}&=\left[\begin{array}{c}0 \\1 \\-2v\end{array}\right]_{(1,2)} =\left[\begin{array}{c}0 \\1 \\-4\end{array}\right] \end{split} \] Detta ger oss att tangenplanet genom vår punkt blir \[ \left[\begin{array}{c}x \\y \\z\end{array}\right]= \left[\begin{array}{c}1 \\0 \\2\end{array}\right]s+ \left[\begin{array}{c}0 \\1 \\-4\end{array}\right]t+\left[\begin{array}{c}1 \\2 \\-3\end{array}\right] \]
Andra ordningens partialderivor
Detta problem hör ihop med föreläsning 2 :: Om Partialderivatan
Uppgift ::
Svar ::
Lösning ::
En enkel dubbelintegral
Detta problem hör ihop med föreläsning 0 :: Från förkunskaper till flervariabelanalys
Uppgift ::
Svar ::
Lösning ::
test av no related lectures
Detta problem är ännu inte kopplad till någon viss föreläsning
Enkla partialderivator
Detta problem hör ihop med föreläsning 0 :: Från förkunskaper till flervariabelanalys
Uppgift ::
Svar ::
Lösning ::
Beräkning av partialderivata
Detta problem hör ihop med föreläsning 0 :: Från förkunskaper till flervariabelanalys