Flervariabelanalys

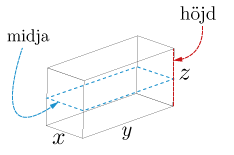
Ett postföretag levererar bara paket i form av rektangulära lådor med midja och höjd uppfyller vissa villkor. Midjan är omkretsen av ett horisontellt tvärsnitt. (Se figur nedan) Vilkoret som paketet måste uppfylla är att summan av midjan och paketets höjd får vara högst 120 cm. Beräkna den största volym som en sådan låda kan ha.

\(x=y=20\)cm, \(z=40\) cm. Volymen blir 16000 \(cm^3\) eller 16 liter.

Vi har den rektangulära lådans sidor givna som \(x\), \(y\) och \(z\). Vår uppgift är att maximera volymen \(V(x,y,z)=x\cdot y\cdot z\) under bivillkoret att \[ \underbrace{2x+2y}_{=\text{ midjan }}+z=120 \] Vi ställer därför upp Lagrangefunktionen: \[ L(x,y,z,\lambda)=xyz-\lambda(2x+2y+z-120). \] Nu söker vi kritiska punkter till Lagrangfunktionen, vilket kräver att vi hittar värden på variablerna som gör att Lagrangefunktionens partialderivator blir noll: \begin{eqnarray*} \frac{\partial L}{\partial x} & = & yz-2\lambda=0 \quad\Rightarrow\quad 2\lambda =yz \\ \frac{\partial L}{\partial y} & = & xz-2\lambda=0\quad\Rightarrow\quad 2\lambda= xz\\ \frac{\partial L}{\partial z} & = & xy-\lambda =0\quad\Rightarrow\quad 2\lambda= 2xy\\ \frac{\partial L}{\partial \lambda} & = & -2x-2y-z+120=0 \end{eqnarray*} De tre första ekvationerna av detta system ger att \(z=2x=2y\) som insatt i bivillkorekvationen (den fjärde partialderivatan till Lagrange) blir \(3z=120\). Vi får att \(x=20\), \(y=20\) och \(z=40\) och den maximala volymen blir således \[ V=20\cdot 20\cdot 40=16\ 000 \ cm^3 \] Uttrycker man sidorna i dm så har vi volymen \[ 2\cdot 2\cdot 4= 16 \ dm^3= 16 \text{ liter} \]